One of the popular applications of exponential functions deals with how things grow or decay as time passes. These applications of exponential growth and decay deal with percentages of increase and percentages of decrease.

In previous courses, you worked with percentages of increase and decrease.

In this lesson, we are going to focus not on "finding" the percent of increase/decrease,
but on "determining a result" based upon a given percent of increase/decrease.

When we worked with linear functions, growth occurred by adding the same amount in each unit of time (thus a constant rate of change). Exponential growth occurs by multiplying by the same factor (percentage) over equal units of time (not a constant rate of change).

Consider this example on percent increase:

Aphids are very small bugs that suck sap from plants.
During the summer, it was initially determined that there were 75 aphids on one plant, and that the rate of increase in this number was 28% per day.

• How many aphids were on the plant after the first day?

Change the percent to a decimal. Multiply times the initial number of aphids to find the number of new day 1 aphids.

28% of 75 = 0.28 • 75 = 21 new aphids in day one.

Add this number of new aphids to the number of initial (old) aphids to find the total number.
75 + 21 = 96 aphids on the plant at the end of day 1.

We can save some time if we combine the two steps we used in our solution, into ONE step!!

Described in ONE step, we did: 75 + 0.28(75) to get the total.
If we factor this ONE step expression, we get 75(1 + 0.28) or 75(1.28).



The 1.28 gives us ALL of the initial amount plus 28% more.

This is an important idea to remember. This strategy will appear in the formula we will be using for exponential growth and decay.

In the table below, notice how the aphid growth is increasing.
Each day the the number of new aphids gets larger.

Starting with 75 aphids , , ,
End of Day 0 1 2 3 4 5 ...
New Aphids 0 21 26 35 44 56 ...
Total Aphids 75 96 122 157 201 257 ...




Consider this example on percent decrease:

Kyle buys a new electric scooter for $590. The value of the scooter will decrease by 30% per year.

• What will be the value of the scooter at the end of one year?

Change the percent to a decimal. Multiply times the initial price of the scooter to find the amount of monetary value lost at the end of one year.

30% of 590 = 0.30 • 590 = $177 lost in value after one year.

Subtract this monetary loss from the price of the new scooter to find the value of the scooter at the end of one year.
590 - 177 = $413 is the value of the scooter after one year.

As we did in the previous example, let's combine the two step process into ONE step!!

Described in ONE step, we did: 590 - 0.30(580) to get the value.
If we factor this ONE step expression, we get 590(1 - 0.30) or 590(0.70).



The 0.70 represents ALL of the initial amount minus 30%.
70% is the % that REMAINS!!

The same strategy was applied in both percent increasing and percent decreasing situations to create a ONE STEP method to solving the problem.

The only difference was that percent increase involved adding,
while the percent decrease involved subtracting.



Before we officially connect these strategies to exponential growth and decay,we need to explore one more component - "time".

In Example 1 (regarding aphids), we discovered that the percent of increase after day one could be expressed as 75(1.28). What happens if we want to continue examining time intervals for not just how many aphids after one day, but how many after each day for several days?

We will need to apply the growth factor (1.28) to the result from each previous day for the designated number of days.

Start: 75 aphids
End of day 1: 75(1.28) = 96 aphids
Now, start with 96, instead of 75:
End of day 2: 96(1.28) = 122.88 = 122 aphids
Now, start with 122.88, instead of 96:
End of day 3: 122.88(1.28) = 157.2864 = 157 aphids
and so on . . .

We know that the 96 at the end of day 1 was calculated by 75(1.28).
The day 2 calculation is 96(1.28).
Replace 96 with 75(1.28) in the day 2 calculation.
The day 2 calculation is now 75(1.28)(1.28) = 75(1.28)2
We have just tied the "time" from the problem to the "exponent" in the calculation.
Day 2 = exponent of 2.

Take another look at multiplying by 1.28 each day:
Start: 75 aphids
End of day 1: 75(1.28) = 75(1.28)1 = 96 aphids
End of day 2: 75(1.28)(1.28) = 75(1.28)2 = 122.88
End of day 3: 75(1.28)(1.28)(1.28) = 75(1.28)3 = 157.2864
and so on . . .

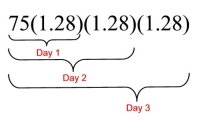Do you see the connection between the exponent and the time intervals?
Day 1 = 1.281
Day 2 = 1.282          The exponent is expressing the time interval.
Day 3 = 1.283


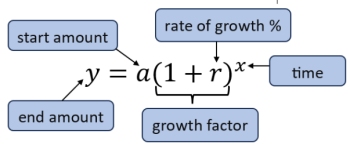
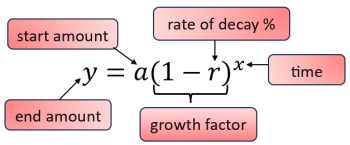
Our strategies have now taken on an exponent
and have become the formulas for exponential growth and exponential decay.

Percent of Increase (Growth)


Add Percentage

Percent of Decrease (Decay)

Subtract Percentage

The letters used to represent the time (x) and the ending amount (y) can change based upon the terms used in a word problem.
The use of x and y used here is a reminder of which variable corresponds to which axis when graphing.

 

divider

NOTE: The re-posting of materials (in part or whole) from this site to the Internet is copyright violation
 and is not considered "fair use" for educators. Please read the "Terms of Use".